A Beginner's Guide to Circumnavigating the Globe

Great circle route around the world starting from Budapest
and passing through China, Oceania and South America

In a previous post, I put together an itinerary to go round the world in thirty-seven days. The itinerary was then successfully implemented in a virtual world tour lasting from the 8^th April to the 15^th May 2013.

I received some criticism, however, for my very “loose” interpretation of the notion of going around the world. My world tour could be considered a circumnavigation of the earth only in one sense: namely, that I arrived back to my starting point after crossing every line of longitude of the planet. It did not fulfil two other criteria that one may expect of a circumnavigation: First, the length of the route did not add up to the circumference of the earth (the whole journey covered around 34.000 km as opposed to 40.000 km, the approximate length of the equator). Second, I came nowhere close to reaching the antipode, i.e. the exact opposite point of my starting place at the other side of the earth; in my case, this would have been in the Southern Pacific, but I did not even leave the northern hemisphere during my journey.

My biggest excuse for these shortcomings is that I followed a great example: Phileas Fogg, Verneʼs hero. Mr Fogg cared just as little with reaching the antipode as myself – although the length of his journey may incidentally have added up to the circumference of the earth due to the circuit he had to make around Asia. In any case, all Fogg had in mind was to come back to London after crossing every line of longitude within 80 days.

Apparently, other people were less impressed by Mr Foggʼs achievement: Norris McWhirter, the founding editor of Guinness World Records went as far as to include the antipode-requirement in a formal definition of a “true circumnavigation.” As he formulated it: “a true circumnavigation of the world must pass through two points antipodean to each other”, i.e. two places on the surface of the globe that are diametrically opposite to each other. Champions of this definition argue that crossing a pair of antipodal points means automatically crossing the equator, traveling the minimum length of the earthʼs circumference, and spending equal time in both the southern and the northern hemispheres. Obviously, neither Foggʼs nor my world tour qualify as a “true circumnavigation”, according to this definition.

Mere scientific criticism of my world tour could have been dismissed easily. Scientific criticism that promotes a circumnavigation “spending equal time in both the southern and the northern hemispheres”, however, is much harder to dismiss. It has some inherent psychological appeal. Who would dispute that a journey through tropical areas and the southern seas is superior to one through Siberia, Alaska, and Newfoundland? In the end, I found myself thinking about how to organize a world tour that passes through “two points antipodean to each other.”

The first discovery I made was that this is not a single-solution problem: not only can anyone have oneʼs own tailor-made world tour, but these world tours – even if starting from the same place – may not have anything in common. In fact, there is an indefinite number of possible routes – of equal length – to get from one antipode to the other. Therefore I decided not to begin with putting together my own itinerary, but with outlining a couple of simple steps that you should follow if you plan a true circumnavigation of the world.

First of all, you have to understand the cause of the inexhaustible variety of world tours. For this purpose, we have to introduce the concept of “great circles.”

Everything You Always Wanted to Know About Great Circles But Were Afraid to Ask 

A great circle is defined as any circle drawn on the surface of the globe with its center coinciding with the center of the globe. Thus, the diameter of a great circle is the same as the globeʼs and the great circle divides the globe into two equal halves. Notable great circles of the earth are the equator and every meridian.

An important characteristic of great circles is that they represent the shortest distance on the globeʼs surface between any two points their segments connect. This is because great circles have the largest radius among curves that can be drawn on the globeʼs surface. The larger a curveʼs radius, the closer it is to a straight line – which is the shortest distance between two given points. Therefore the segment of the great circle falling between the two given points represents the shortest distance between the two points on the globeʼs surface.

Because of this, great circles have been important in navigation for hundreds of years. They are still used in long distance travel as the most efficient way to move across the globe – at least where wind and water currents do not play a significant role. In the northern hemisphere, for example, airplanes traveling west normally follow a great circle route over the Arctic – whereas they use the rapid eastward airflow of the jet stream when traveling eastbound.

Great circles transform to straight lines via gnomonic
projection. Credit: Marozols

In the past, the easiest way to find the great circle route between two given points was to draw a straight line between the two points on a gnomonic map projection. A gnomonic map displays all great circles as straight lines. This is because it projects each surface point of the globe onto a tangent plane from a perspective point located at the center of the globe. Since points of a great circle and the center of the globe are situated on the same plane by definition, rays emanating from the center of the globe that pass through points of a given great circle will always be on a single plane. The intersection of the plane so defined and the tangent plane will necessarily be a straight line. This straight line is the great circle segment as projected onto the tangent plane.

This gnomonic map, centered on the North Pole, was plotted by American cartographer Richard Edes Harrison in 1943 in order to raise the awareness of the American public for the proximity of the US to Germany and to the Soviet Union through great circle routes over the Arctic. (Publisher: Time, Inc., downloaded from the Norman B. Leventhal Map Center.) Harrison connected some cities with straight lines, indicating the shortest route between them. I drew straight lines myself from Budapest to Manila (with red) and to Panama (with yellow) showing the great circle routes leading to these places.

The gnomonic map in itself is unsuitable for navigation, however. One reason for this is that the gnomonic projection can depict less than a hemisphere of the globe on a single map: even the edge of the depicted hemisphere lies in infinity. Accordingly, regions close to the edge are extremely distorted both in shape and in areas. The other, more important reason is that the course to follow is difficult to determine based on a gnomonic map. For centuries, people used the compass to define the direction they should be heading to reach their destination. On a great circle route, however, the compass direction (the course to follow as compared to north) will continually change (the route will cross meridians at a continuously changing angle). While it is possible to get an idea of this changing compass direction by looking at the gnomonic map, it is by far not the most suitable way of determining the actual course to follow. There is a much better solution: it is called the Mercator projection.

The Mercator projection was designed by the Flemish cartographer Gerardus Mercator in 1569 precisely for navigation purposes. It has the unique feature of representing routes of constant compass direction as straight lines. This is achieved by two important characteristics of the projection: First, it depicts the globe as a rectangular coordinate-system with an east-west and a north-south axis, in which every meridian makes a right angle with every line of latitude. This characteristic, which is common to all normal cylindrical projections, suits the frame of reference of a compass. Second, the Mercator-projection stretches latitudes (north-south distances) in the same proportion as it stretches longitudes (east-west distances). The east-west stretching of distances away from the equator follows necessarily from the characteristic of normal cylindrical projections that they represent all lines of latitude as having the same length – although these in fact become ever shorter approaching the poles. By applying the same stretching also to north-south distances, the Mercator-projection provides conformality (the preservation of angles) at the expense of the equality of areas – which become extremely distorted at higher latitudes.

As a consequence of conformality, a straight line drawn on the Mercator-map between two points will show the direction in which the two points are located as compared to north. The line defined by this “true compass direction” will make the same angle with every meridian it crosses. If you follow this route, therefore, the compass direction will be constant throughout the journey. Since you need not regularly adjust the course, navigation is much easier.

Of course, the route defined by constant compass direction will in most cases be different, and therefore longer, than the great circle route. At longer distances and on higher latitudes, the difference between the two routes may be significant both in path and in length.

Routes from Budapest to Manila on a Mercator-map. The red line shows
the great circle route (also called "orthodrome") taken manually from
 the gnomonic map above. The blue line represents the constant course
 route (also called "loxodrome"). 

It is possible, however, to plot the great circle route on a Mercator-map. In this case you will have the best of both worlds: the shortest route – depicted in a way that shows how the course is changing along it. Such a mapping can be achieved by taking the great circle line drawn on the gnomonic map, noting a number of points along it (e.g., where it crosses a shoreline, a river or a meridian), then plotting the same points on the Mercator map and connecting them with a smooth curve. Please note that the resulting line will appear curved on the Mercator map and will therefore look longer than the straight line between the same points (representing the constant course route). In reality, the great circle route (represented by the curved line) is the shorter.

All roads lead to the antipode 

Between any given starting point and most other points, there is only one – uniquely definable – great circle route. For any given starting point, however, there is one point on the surface of the globe to which an indefinite number of great circle routes lead: the starting pointʼs antipode. This truth, which is only natural, may be difficult to recognize because one is inclined to think in the terms of the Mercator-map: One would look for the true compass direction to determine the route leading to the antipode – and the true compass direction would be uniquely definable. If one planned to get to the other side of the Earth from Budapest, for example, the true compass direction to follow would be around 121º eastbound or 239º westbound (where 0º is North, 90º is East, 180º is South and 270º is West).

In contrast to this, an indefinite number of great circle routes exist that lead to a starting pointʼs antipode. This truth can best be visualized on the example of the poles. Obviously, you can get from the North Pole to the South Pole by following any meridian – and every meridian is a great circle with the same length. Between other antipodal points you can similarly draw great circle routes through any arbitrarily selected third point on the surface of the globe. The reason for this is simple: Any great circle drawn from a given starting point has to pass through the pointʼs antipode, that is, where the globeʼs diameter drawn through the starting point intersects the other side of the globe. Otherwise it would not be a great circle. 

You can check this thesis with the help of modern technology. Today you no longer need a gnomonic map to find the great circle route between two places: you can use a great circle mapping software instead. With such a software you can also conduct the following experiment: Enter two antipodal points as the start and end points of the route and any third point as an

intermediate station. Let the software draw the great circle route between the given points. When looking at the result you will notice two things: First, that the line of the route is not broken at the intermediate station – suggesting that the intermediate point lies on the great circle segment connecting the start and end points. Second, that the length of the route is about half of the

circumference of the Earth – suggesting, again, that the line drawn between the antipodal points is half of a great circle. Now repeat the above steps with different intermediate stations. The results will be similar: smooth curves through the intermediate stations with a length of half of the Earthʼs circumference. All the lines drawn this way will be great circle segments connecting the

two antipodal points through the arbitrarily selected intermediate station. This proves that there is an indefinite number of great circle routes leading to a pointʼs antipode.

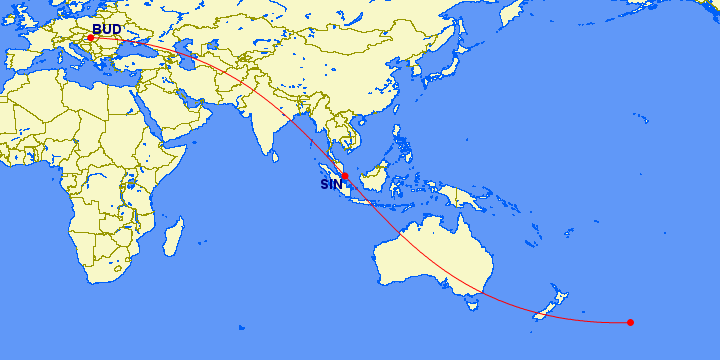From Budapest, for example, you can draw great circle routes via Helsinki, Vladivostok, Singapore, Nairobi, Rio de Janeiro, Lima, or Chicago, all

leading to the cityʼs antipode. The length of these routes vary from 20 005 km to 20 020 km, i.e. around the half of the earthʼs circumference (the routes passing through the polar regions being somewhat shorter because the earth is flattened along the axis). In contrast, the constant course route between Budapest and its antipode would be 20564 km long, i.e. around 560 km longer than

Great circle routes from Budapest to its antipode through
Helsinki, Vladivostok, Singapore, Nairobi, Rio de Janeiro
and Chicago

any great circle route. The difference is not very big because the constant course route goes mostly through low latitudes, where its frame of reference is consisted of lines of latitude and longitude that are either great circles themselves or are pretty close to it.

After this short introduction into the theory of great circles, the steps of planning the route of a true circumnavigation are pretty straightforward.

Step 1 : Choose the pair of antipodal points you would like to pass through

A bit counterintuitively, the antipodes do not necessarily have to include your starting point: What matters is that you pass through a pair of antipodal points along the way, no matter where they are located on the route. It is practical, however, to have both antipodes on land and not on sea because it is difficult for an ordinary person to get to a certain place on sea if he or she does not own a ship. In effect, this imposes serious restriction on the available set of antipode-pairs: as 71% of the earthʼs surface is covered by sea, it is not easy to find two places exactly opposite to each other that are both on land.

You can try on the following webpage: http://www.findlatitudeandlongitude.com/antipode-map. As you will see, possible pairs of antipodes include: the South Sahara in Mali – the Fiji Islands on the Pacific; Rajasthan province, India – Easter Island; Buryatia, Russia – Tierra del Fuego, South America; Beijing – Rio Negro province, Argentina; Singapore – East Ecuador; Montana, U.S. – the Kerguelen Islands on the Southern Indian Ocean. Europe almost completely lacks any antipodal points situated on land – the exception being the Iberian Peninsula, which has antipodes on New Zealand. If you start from Europe and want to get to the other side of the earth, I recommend a pair of antipodes formed by the Sevilla region, Spain – and Auckland, New Zealand. If getting to the other side of the planet is not important to you, on the other hand, you can find a wide choice of comfortably located antipode-pairs on the Far East – South America axis.

Step 2: Choose the region through which you would like to get from one antipode to the other

As the location of the antipodes does not determine the route in any significant way, this is really a choice up to you. You may prefer the most exotic regions or fast transport networks or you may want to see as much on the way as you can. You can then draw a great circle route between the two antipodes through the selected region as intermediate station.

Assume, for example, that the antipodes you selected are Sevilla and Auckland. You can take a rather exotic route through the Arabian Peninsula. Or you may like the idea that you can get from Europe to China pretty fast by train. Or you may be bent on making most of the journey on land and therefore decide to go through India. For each of these selections, you can draw the great circle route, which will show you the shortest way from Sevilla to Auckland through the chosen region. You may even make your final decision concerning the direction after comparing these routes.

You can repeat the same exercise for the return journey on the other hemisphere.

Step 3: Prepare the detailed itinerary based on the great circle route

Of course, the great circle route drawn this way represents only an “ideal” way to get from one antipode to the other. You will need to deviate from this route to some extent depending on the available transport options. This “practical” side of planning a true circumnavigation will be discussed on the example of my own “antipodean” world tour to be presented in a later post.